给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
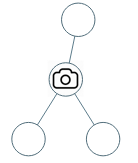
输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
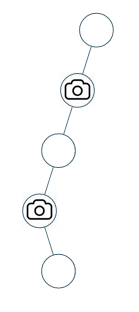


输入:[0,0,null,0,null,0,null,null,0] 输出:2 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
**难度**: Hard
**标签**: 树、 深度优先搜索、 动态规划、
# -*- coding: utf-8 -*-
# @Author : LG
"""
执行用时:60 ms, 在所有 Python3 提交中击败了64.62% 的用户
内存消耗:13.8 MB, 在所有 Python3 提交中击败了6.61% 的用户
解题思路:
后序遍历,先处理左右子树。将子树为空看做子树已覆盖。
当前节点存在以下状态:
1. 叶节点,左右子树为空。看做当前节点左右子树均已覆盖,则当前节点忽略
2. 左右子树存在子树不覆盖,则当前节点放置监控
3. 如果左右子树放置监控,则当前节点已覆盖
4. 如果当前节点是根节点,且左右子树已覆盖,需在当前节点放置监控
"""
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def minCameraCover(self, root: TreeNode) -> int:
self.result = 0
def find(now_root):
if now_root.left:
find(now_root.left)
if now_root.right:
find(now_root.right)
l_val, r_val = 1, 1
if now_root.left: # 左子树不为空,处理左子树
l_val = now_root.left.val
if now_root.right: # 右子树不为空,处理右子树
r_val = now_root.right.val
if not (r_val and l_val): # 如果左右子树存在未覆盖节点,则当前节点 放置监控
now_root.val = 2
self.result += 1
elif now_root == root and l_val != 2 and r_val != 2: # 如果子树已覆盖,但当前节点为根,则需单独放置一个监控
print(now_root)
self.result += 1
elif r_val == 2 or l_val == 2: # 如果左右子树中放置了监控,则当前节点被覆盖
now_root.val = 1
if root.left or root.right:
find(root)
return self.result
else:
return 1
